By: Jeremy Neisser
Cavity filters are a type of electronic filter that are widely used in various applications, including wireless communication, radar systems, and satellite communication. These filters are designed to selectively pass or reject signals based on their frequency, and are capable of providing high levels of attenuation to unwanted signals.
In this article, I will provide an overview of cavity filters, including their fundamentals, types, design considerations, performance metrics, applications, manufacturing and quality assurance, installation and maintenance, and frequently asked questions.
What are Cavity Filters
At their core, cavity filters are resonant structures that use the principles of electromagnetic wave propagation to selectively pass or reject signals. These filters are typically made up of a series of resonant cavities, which are essentially hollow metal structures that are designed to resonate at a particular frequency.
The cavities are usually coupled together using small holes or slots, which allow the signals to pass through the filter while providing high levels of attenuation to unwanted signals.
There are various types of cavity filters available, each with their own unique design considerations and performance metrics. Some of the most common types include coaxial cavity filters, waveguide cavity filters, and microstrip cavity filters. The choice of filter type will depend on the specific application requirements, such as frequency range, insertion loss, and selectivity.

Fundamentals of Cavity Filters
Definition and Purpose
Cavity filters are electronic devices that are used to selectively allow certain frequencies to pass through while blocking others. They are commonly used in communication systems, such as radios and televisions, to filter out unwanted signals and noise.
The purpose of cavity filters is to provide a high level of selectivity and frequency stability. They are able to achieve this by using resonant cavities, which are enclosed metallic structures that are designed to resonate at a specific frequency.
Basic Operating Principles
Cavity filters operate based on the principle of resonance. When an electrical signal is applied to the cavity, it will resonate at the frequency that it is designed for. This resonance causes the cavity to have a high impedance at the resonant frequency, which allows the signal to pass through while blocking other frequencies.
The selectivity of a cavity filter is determined by the number of resonant cavities used in the filter. The more cavities that are used, the higher the selectivity of the filter.
Key Components
The key components of a cavity filter include the resonant cavities, coupling loops, and input/output ports. The resonant cavities are the enclosed metallic structures that are designed to resonate at a specific frequency. The coupling loops are used to transfer energy between the cavities, while the input/output ports are used to connect the filter to the rest of the circuit.
In addition to these components, cavity filters may also include tuning screws and capacitors, which are used to adjust the resonant frequency of the cavities.
Overall, cavity filters are an essential component in many communication systems, providing high levels of selectivity and frequency stability.
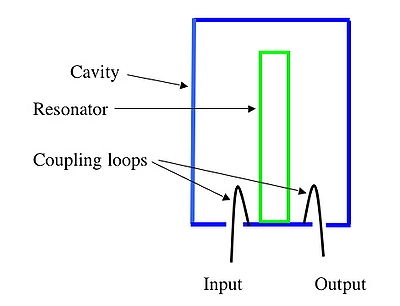
via www.amateur-radio-wiki.net
Most cavity filters consist of 4 basic parts:
- 1Input line (feeds the signal into the cavity)
- 2Output line (captures filtered signal coming out of resonant cavity)
- 3Feedthrough capacitor(s) (allows DC current to flow through cavity)
- 4A ground connection
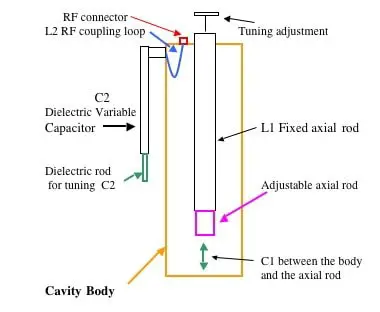
www.amateur-radio-wiki.net
Types of Cavity Filters
Bandpass Cavity Filters
Bandpass cavity filters are used to allow a specific range of frequencies to pass through while rejecting all others. These filters are designed using a resonant cavity that has a narrow bandwidth. The bandwidth of the filter is determined by the Q factor of the cavity. The higher the Q factor, the narrower the bandwidth.
Bandpass cavity filters are commonly used in radio and communication systems. They are used to select a particular frequency from a range of frequencies. These filters are also used in microwave systems to remove unwanted signals and noise.
Bandstop Cavity Filters
Bandstop cavity filters, also known as notch filters, are used to reject a specific range of frequencies while allowing all others to pass through. These filters are designed using a resonant cavity that has a wide bandwidth. The bandwidth of the filter is determined by the Q factor of the cavity. The lower the Q factor, the wider the bandwidth.
Bandstop cavity filters are commonly used in communication systems to remove unwanted signals and noise. They are also used in microwave systems to reject interference from other sources.
In summary, cavity filters are used in various applications to allow or reject specific frequencies. Bandpass cavity filters allow a particular range of frequencies to pass through while bandstop cavity filters reject a specific range of frequencies. The design of these filters is based on the resonant cavity and the Q factor of the cavity determines the bandwidth of the filter.
Design Considerations
Resonator Design
When designing cavity filters, the resonator design is a crucial consideration. The resonator determines the filter's frequency response and selectivity. The resonator's shape and dimensions determine its resonant frequency, which should be precisely tuned to the desired frequency. The resonator's Q factor also affects the filter's selectivity, with higher Q factors resulting in narrower bandwidths. The resonator's material choice and fabrication method also play a role in the filter's performance and cost.
Coupling Mechanisms
The coupling mechanism is another critical design consideration for cavity filters. The coupling mechanism determines how energy is transferred between resonators and affects the filter's coupling coefficient and insertion loss. The most common coupling mechanisms for cavity filters are iris coupling and loop coupling. Iris coupling uses a small aperture in the resonator walls to couple energy between resonators, while loop coupling uses a wire loop to couple energy between resonators. The choice of coupling mechanism depends on the filter's requirements and the resonator's geometry.
Tuning and Adjustment
Tuning and adjustment are essential considerations for cavity filters, as they affect the filter's performance and reliability. The resonator's dimensions and coupling mechanism determine the filter's frequency response, and any deviations from the desired frequency response require tuning and adjustment. Tuning and adjustment can be achieved by adjusting the resonator's dimensions or by adding tuning screws or capacitors. The tuning and adjustment process must be carefully controlled to ensure the filter's performance meets the required specifications.
Performance Metrics
Insertion Loss
One of the key performance metrics of cavity filters is the insertion loss, which is the amount of signal power lost as a result of the filter. The insertion loss of a cavity filter is determined by the quality factor (Q) of the resonant cavity and the coupling coefficient between the cavity and the input/output ports. Generally, the higher the Q factor, the lower the insertion loss.
Bandwidth and Selectivity
Another important performance metric of cavity filters is bandwidth and selectivity. Bandwidth is the range of frequencies that the filter can pass with a specified level of attenuation, while selectivity is the ability of the filter to distinguish between closely spaced frequencies. Cavity filters can achieve high selectivity by using several resonant cavities in series or parallel, which create a narrow passband and high attenuation outside the passband.
Rejection and Return Loss
Cavity filters also have excellent rejection capabilities, which is the ability to attenuate signals outside the passband. Rejection is determined by the number of resonant cavities used and the coupling between the cavities. Return loss, which is the amount of reflected power at the input/output ports, is also an important performance metric of cavity filters. High return loss indicates good impedance matching between the filter and the system.
In summary, cavity filters offer superior performance metrics such as low insertion loss, high selectivity, excellent rejection, and high return loss, making them ideal for a wide range of applications in wireless communication systems.
Applications of Cavity Filters
Wireless Communication Systems
Cavity filters play a crucial role in wireless communication systems by filtering out unwanted signals and interference. They are used in a wide range of applications, including cellular networks, Wi-Fi, Bluetooth, and other wireless technologies. Cavity filters are essential in ensuring that wireless communication systems operate efficiently and without interference.
Satellite Communication
Satellite communication systems rely on cavity filters for signal filtering and interference rejection. Cavity filters are used in satellite transponders to filter out unwanted signals and interference, ensuring that the signals transmitted and received are of high quality and free from interference. Cavity filters are also used in satellite ground stations to filter out unwanted signals and interference.
Military and Defense
Cavity filters are widely used in military and defense applications, where they are used to filter out unwanted signals and interference. They are used in radar systems, communication systems, and electronic warfare systems. Cavity filters are essential in ensuring that military and defense systems operate efficiently and without interference, making them a critical component in national security.
In summary, cavity filters are essential components in various applications, including wireless communication systems, satellite communication, and military and defense systems. They play a crucial role in ensuring that signals are of high quality and free from interference, making them critical in various industries.
Manufacturing and Quality Assurance
Fabrication Techniques
Cavity filters are manufactured using various techniques, including etching, milling, and casting. The choice of technique depends on the required specifications, such as the frequency range, insertion loss, and power handling capability.
Etching is a commonly used technique, where a thin layer of metal is deposited on a substrate and then selectively removed using a chemical process. This technique is suitable for producing high Q-factor filters with low insertion loss. Milling, on the other hand, involves cutting away the unwanted material from a solid block of metal. This technique is suitable for producing filters with complex geometries and tight tolerances.
Casting is another technique used for producing cavity filters. In this technique, molten metal is poured into a mold and allowed to solidify. This technique is suitable for producing large filters with irregular shapes.
Testing Procedures
Quality assurance is an important aspect of cavity filter manufacturing. Various testing procedures are employed to ensure that the filters meet the required specifications.
One of the most common testing procedures is the insertion loss measurement. This involves measuring the loss of signal power as it passes through the filter. The lower the insertion loss, the better the performance of the filter.
Another important testing procedure is the return loss measurement. This involves measuring the amount of power that is reflected back from the filter. A high return loss indicates that the filter is well-matched to the input and output ports.
Other testing procedures include power handling capability, temperature stability, and vibration resistance. These tests ensure that the filters can operate reliably under different conditions.
In conclusion, the manufacturing and quality assurance of cavity filters require careful attention to detail and adherence to strict specifications. By employing various fabrication techniques and testing procedures, manufacturers can ensure that the filters meet the required performance standards.
Installation and Maintenance
Mounting and Integration
When installing cavity filters, it is important to consider the physical space available and the frequency range required. The filters should be mounted securely to prevent any movement or damage during operation. It is recommended to use a mounting bracket or a flange to attach the filter to the system.
Integration of the cavity filter into the system should be done carefully to avoid any unwanted coupling or interference. It is essential to follow the manufacturer's instructions and specifications to ensure proper performance. In addition, checking the impedance matching and tuning the filter may be necessary to optimize the system's performance.
Troubleshooting and Repair
If the cavity filter is not functioning as expected, it may require troubleshooting and repair. The first step is to check the connections and wiring to ensure proper installation. If the issue persists, it may be necessary to perform a frequency sweep or impedance measurement to identify the problem.
In some cases, the cavity filter may require repair or replacement of components. It is recommended to contact the manufacturer or a qualified technician for repair services. Attempting to repair the filter without proper knowledge and tools may cause further damage or safety hazards.
Regular maintenance of the cavity filter is essential to ensure optimal performance and longevity. This includes checking the connections, cleaning the filter, and inspecting for any physical damage. It is recommended to follow the manufacturer's guidelines for maintenance and to schedule periodic inspections by a qualified technician.
You might like: CB Radio Frequencies with PDF
Frequently Asked Questions
How do cavity filters function in RF applications?
Cavity filters are resonant devices that operate based on the principle of electromagnetic wave resonance. They consist of a series of conductive plates that form a resonant cavity, which is tuned to a specific frequency of operation. The input signal is coupled into the cavity, where it resonates at the desired frequency, while filtering out unwanted frequencies.
What distinguishes cavity filters from SAW filters in performance and usage?
Cavity filters offer superior performance in terms of insertion loss and selectivity, making them ideal for high-performance RF applications. SAW filters, on the other hand, are smaller and more compact, making them suitable for low-power, mobile applications.
What are the typical insertion losses for cavity filters in communication systems?
The insertion loss of a cavity filter depends on various factors, such as the frequency of operation, the number of resonant cavities, and the quality factor of the resonant cavities. In general, cavity filters offer low insertion loss, typically in the range of 0.5 to 1 dB.
Can cavity filters be used for high-power signal filtering, and what are the limitations?
Yes, cavity filters can be used for high-power signal filtering, but their power handling capability is limited by the breakdown voltage of the dielectric material used in the resonant cavities. The power handling capability can be increased by increasing the size of the resonant cavities and using high-quality dielectric materials.
What parameters are critical when designing an RF cavity filter for specific frequencies?
The critical parameters for designing an RF cavity filter include the resonant frequency, the bandwidth, the insertion loss, the selectivity, the power handling capability, and the size of the resonant cavities. These parameters can be optimized based on the specific requirements of the application.
How does the physical size of a cavity filter relate to its operational frequency?
The physical size of a cavity filter is directly proportional to its operational frequency. This is because the size of the resonant cavities determines the resonant frequency of the filter. As the size of the resonant cavities decreases, the resonant frequency of the filter increases.
- You May Like - The Most Popular/Best Handheld CB Radios

Hi & Welcome!
My name is Jeremy and I have been an avid car nut for many year. My first car was an 1987 Honda CRX. I put in my first Kenwood stereo, amp, 2 10" JLs and a CB Radio in it and have been an avid user of CBs and car radios for years. I'll do my best to share my tips, information and thoughts to help you with whatever question you might have, ABOUT ME
After I graduated from High School, I worked 5 years are Radio Shack and 3 years at Circuit City answering questions and helping customers with various electronics questions.

